【十大经典数据挖掘算法】系列
SVM(Support Vector Machines)是分类算法中应用广泛、效果不错的一类。《统计学习方法》对SVM的数学原理做了详细推导与论述,本文仅做整理。由简至繁SVM可分类为三类:线性可分(linear SVM in linearly separable case)的线性SVM、线性不可分的线性SVM、非线性(nonlinear)SVM。
1. 线性可分
对于二类分类问题,训练集\(T = \lbrace (x_1,y_1),(x_2,y_2), \cdots ,(x_N,y_N) \rbrace\),其类别\(y_i \in \lbrace 0,1 \rbrace\),线性SVM通过学习得到分离超平面(hyperplane):
\[ w \cdot x + b =0 \]
以及相应的分类决策函数:
\[ f(x)=sign(w \cdot x + b) \]
有如下图所示的分离超平面,哪一个超平面的分类效果更好呢?
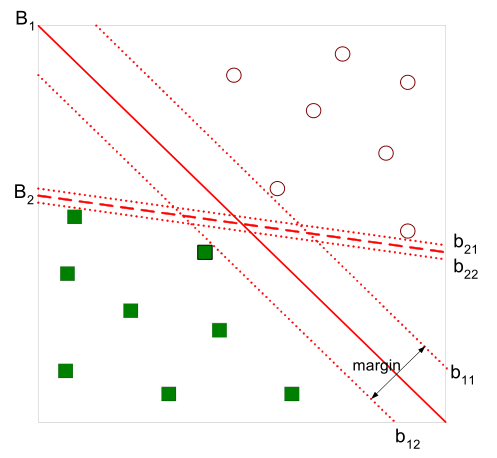
直观上,超平面\(B_1\)的分类效果更好一些。将距离分离超平面最近的两个不同类别的样本点称为支持向量(support vector)的,构成了两条平行于分离超平面的长带,二者之间的距离称之为margin。显然,margin更大,则分类正确的确信度更高(与超平面的距离表示分类的确信度,距离越远则分类正确的确信度越高)。通过计算容易得到:
\[ margin = \frac{2}{\|w\|} \]
从上图中可观察到:margin以外的样本点对于确定分离超平面没有贡献,换句话说,SVM是有很重要的训练样本(支持向量)所确定的。至此,SVM分类问题可描述为在全部分类正确的情况下,最大化\(\frac{2}{\|w\|}\)(等价于最小化\(\frac{1}{2}\|w\|^2\));线性分类的约束最优化问题:
\begin{align}
& \min_{w,b} \quad \frac{1}{2}|w|^2 \cr & s.t. \quad y_i(w \cdot x_i + b)-1 \ge 0 \label{eq:linear-st} \end{align}对每一个不等式约束引进拉格朗日乘子(Lagrange multiplier)\(\alpha_i \ge 0, i=1,2,\cdots,N\);构造拉格朗日函数(Lagrange function):
\begin{equation}
L(w,b,\alpha)=\frac{1}{2}|w|^2-\sum_{i=1}^{N}\alpha_i [y_i(w \cdot x_i + b)-1] \label{eq:lagrange} \end{equation}根据拉格朗日对偶性,原始的约束最优化问题可等价于极大极小的对偶问题:
\[ \max_{\alpha} \min_{w,b} \quad L(w,b,\alpha) \]
将\(L(w,b,\alpha)\)对\(w,b\)求偏导并令其等于0,则
\[ \begin{aligned} & \frac{\partial L}{\partial w} = w-\sum_{i=1}^{N}\alpha_i y_i x_i =0 \quad \Rightarrow \quad w = \sum_{i=1}^{N}\alpha_i y_i x_i \cr & \frac{\partial L}{\partial b} = \sum_{i=1}^{N}\alpha_i y_i = 0 \quad \Rightarrow \quad \sum_{i=1}^{N}\alpha_i y_i = 0 \end{aligned} \]
将上述式子代入拉格朗日函数\eqref{eq:lagrange}中,对偶问题转为
\[ \max_{\alpha} \quad -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^{N}\alpha_i \]
等价于最优化问题:
\begin{align}
\min_{\alpha} \quad & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i \cr s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr & \alpha_i \ge 0, \quad i=1,2,\cdots,N \end{align}线性可分是理想情形,大多数情况下,由于噪声或特异点等各种原因,训练样本是线性不可分的。因此,需要更一般化的学习算法。
2. 线性不可分
线性不可分意味着有样本点不满足约束条件\eqref{eq:linear-st},为了解决这个问题,对每个样本引入一个松弛变量\(\xi_i \ge 0\),这样约束条件变为:
\[ y_i(w \cdot x_i + b) \ge 1- \xi_i \]
目标函数则变为
\[ \min_{w,b,\xi} \quad \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{N} \xi_i \]
其中,\(C\)为惩罚函数,目标函数有两层含义:
- margin尽量大,
- 误分类的样本点计量少
\(C\)为调节二者的参数。通过构造拉格朗日函数并求解偏导(具体推导略去),可得到等价的对偶问题:
\begin{equation}
\min_{\alpha} \quad \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} {\alpha_i} \label{eq:svmobj} \end{equation}\begin{align}
s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr & 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N \end{align}与上一节中线性可分的对偶问题相比,只是约束条件\(\alpha_i\)发生变化,问题求解思路与之类似。
3. 非线性
对于非线性问题,线性SVM不再适用了,需要非线性SVM来解决了。解决非线性分类问题的思路,通过空间变换\(\phi\)(一般是低维空间映射到高维空间\(x \rightarrow \phi(x)\))后实现线性可分,在下图所示的例子中,通过空间变换,将左图中的椭圆分离面变换成了右图中直线。
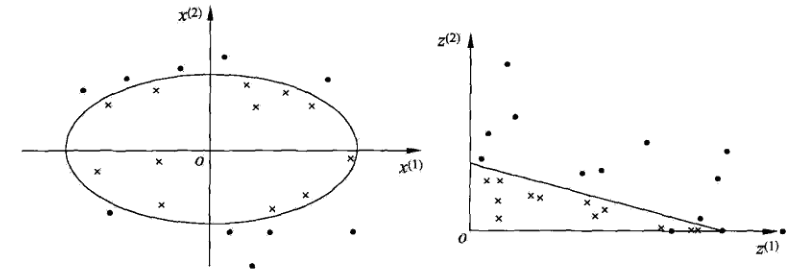
在SVM的等价对偶问题中的目标函数中有样本点的内积\(x_i \cdot x_j\),在空间变换后则是\(\phi(x_i) \cdot \phi(x_j)\),由于维数增加导致内积计算成本增加,这时核函数(kernel function)便派上用场了,将映射后的高维空间内积转换成低维空间的函数:
\[ K(x,z)=\phi(x) \cdot \phi(z) \]
将其代入一般化的SVM学习算法的目标函数\eqref{eq:svmobj}中,可得非线性SVM的最优化问题:
\begin{align}
\min_{\alpha} \quad & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i,x_j) - \sum_{i=1}^{N}\alpha_i \cr s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr & 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N \end{align}4. 参考资料
[1] 李航,《统计学习方法》.
[2] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, .